
Numeriske gåder til din hjerne

Numeriske gåder til din hjerne
I denne guide tilbyder vi en række praktiske tips til, hvordan man løser Kakuro-gåder, med sværhedsgrader fra begynder- til ekspertniveau.
For at opsummere reglerne: Kakuro er et puslespil på et krydsordslignende bræt, hvor cifre bruges til at summere sig til værdier angivet i 'definitions'-felterne på brættet. Derudover må hvert ciffer højst forekomme én gang inden for hver sumgruppe.
Den traditionelle måde at løse en Kakuro-gåde på er trinvis: ved at bruge den eksisterende information på brættet kan du med sikkerhed finde værdien af en specifik celle, som kun kan antage én mulig værdi. Derefter udfyldes denne værdi, og processen gentages, indtil alle brætcellerne er blevet opdaget.
I nogle situationer er der ingen specifik bestyrelsescelle, der kun har én mulighed. I disse tilfælde skal hver af mulighederne udforskes for sig selv og elimineres gennem modsætninger, indtil kun én handlingsmulighed er tilbage.
Vi præsenterer nedenfor flere metoder til at komme videre i løsningen af selve gåden.
Der er nogle definitioner, der kun kan løses på en specifik måde:
og så videre... Normalt kan du holde musen over definitionstallet på et Kakuro-gitter, og et værktøjstip vil dukke op med alle mulighederne for at skrive den sum med unikke cifre i antallet af tilgængelige celler.
De summer, der kan skrives på en unik måde, er normalt lave summer eller høje summer, der tvinger lave/høje cifre i svaret for at opnå dem.
Det hjælper at have en unik måde at skrive summen på, men husk at alle permutationer er gyldige, og du skal stadig finde ud af, hvilken faktisk permutation du skal bruge på tavlen.
 |
 |
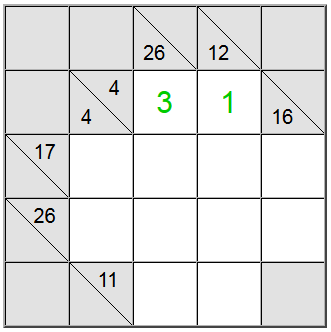 |
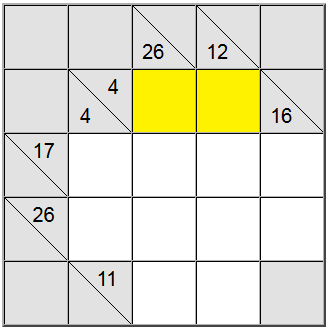
For de gule celler, der er fremhævet ovenfor, er der kun én måde at skrive summen på: 4 = 1 + 3. Vi skal dog stadig finde ud af, hvilken permutation (1 + 3 eller 3 + 1) vi skal bruge.
Det viser sig, at definitionen af 26 vertikalt hjælper os: en sum på tværs af 4 celler, der ville indeholde cifferet 1, ville højst være 1 + 9 + 8 + 7 = 25. Da vores sum er 26, viser det sig, at cifferet 1 ikke kan være en del af summen. Derfor er den eneste tilbageværende rækkefølge for de gule firkanter 3 + 1.
 |
 |
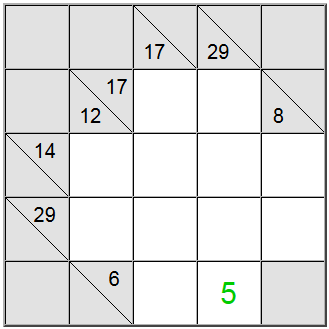 |
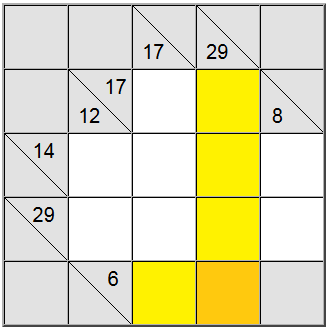
På tavlen ovenfor kan de vandrette gule firkanter skrives som 6 = 1 + 5 eller 6 = 2 + 4. Den lodrette gule sum kan kun skrives som 29 = 5 + 7 + 8 + 9.
Den gule firkant, der findes i skæringspunktet mellem disse to sumdefinitioner, skal indeholde det samme ciffer, så der skal være et fælles ciffer til stede i de vandrette og lodrette definitioner for at kunne deles mellem dem. Ved at se på mulighederne ovenfor kan vi nemt finde ud af, at 5 er det eneste ciffer, der overholder dette kriterium.
Denne teknik fungerer især godt, når man krydser en definition med en lav sum og en definition med en høj sum. Definitioner med lav sum og høj sum er dem, der har et relativt lavt eller højt definitionstal (henholdsvis 6 og 29 i vores eksempel) sammenlignet med antallet af tilgængelige celler. Fordi 6 er relativt lavt, vil det tvinge lave cifre i sumrepræsentationen, og 29 vil tvinge høje cifre (for at opnå disse summer ved hjælp af det givne antal celler). Derfor vil skæringspunktet mellem lave og høje cifre sandsynligvis kun indeholde én kandidat til den faktiske celleværdi.
 |
 |
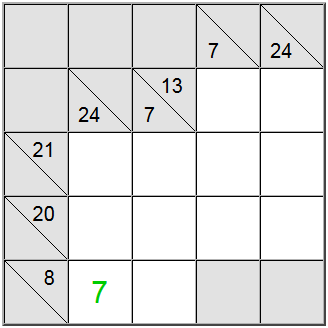 |
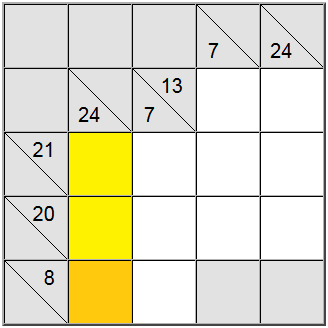
Nogle gange er det nyttigt at finde ud af den maksimale eller minimale værdi for en sumgruppe. Dette kan give dig en fornemmelse af, hvad der er det gyldige cifferinterval for den pågældende sum, hvilket igen vil hjælpe dig med at lave korrelationer med andre begrænsninger og finde ud af de unikke tildelinger på brættet.
I eksemplet ovenfor accepterer de gule lodrette celler kun værdier lig med 7 eller højere. Hvis du forsøger at tildele et 6, kan du nemt finde ud af, at 6 + 9 + 8 = 23, så definitionssummen på 24 ville ikke være opnåelig.
Fordi 7 er et minimum, tvinger den horisontale definition, der har 8 som sum, 7'eren i den position.
Øvelse er den bedste måde at se, hvordan disse råd kan anvendes i rigtige Kakuro-spil. Spil et puslespil for alvor. Vi ønsker dig held og lykke og masser af sjov!
© 2026 - Alle rettigheder forbeholdes - Kontaktside - Privatlivspolitik - DA | DE | EN | ES | FR | IT | JA | LT | LV | NL | PL | PT | RO | SV | TR